이동 평균 필터 (Moving average filter)
튄 데이터 값을 보정(평활화)하는 이동 평균 필터 알고리즘에 대해 알아보자
Github
본 포스팅에 작성된 소스코드와 예시 데이터는 깃허브에 공개되었습니다.
GitHub - SpiralMoon/moving_average_filter: Move Average Filter
Move Average Filter. Contribute to SpiralMoon/moving_average_filter development by creating an account on GitHub.
github.com
이동 평균 필터링이란?
이동 평균 필터링은 연속된 데이터에서 인접한 n개 데이터의 평균을 구하여 순차적으로 데이터를 필터링하는 기법이다.
연속된 데이터가 급격하게 변화할 때 이를 완화시켜주는 효과가 있다.

예시 데이터에서 최근 3개 데이터의 평균을 구하는 이동 평균 필터는 다음과 같이 동작한다. (3 = 버퍼의 크기)
아래 예시에서 필터링이 동작하는 방식을 그림으로 설명하고 있다. 검은 박스는 버퍼, 초록 박스는 결과값이다.
첫 번째 루프

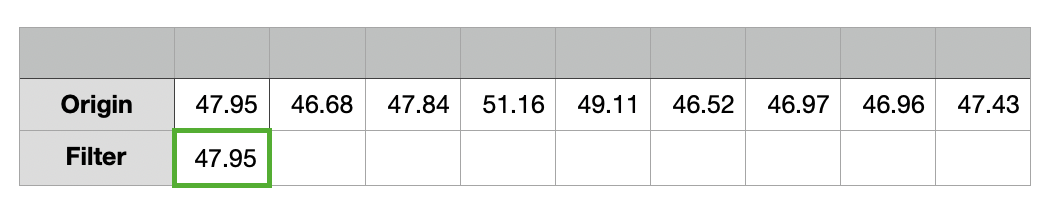
첫 번째 루프에서는 버퍼의 크기가 3이지만 1번째 데이터만 식별되므로
= (Origin[0]) / (buffer의 요소 개수)
= 47.95 / 1
= 47.95
필터링의 결과는 47.95이다.
두 번째 루프


두 번째 루프에서는 버퍼의 크기가 3이지만 1, 2번째 데이터만 식별되므로
= (Origin[0] + Origin[1]) / (buffer의 요소 개수)
= (47.95 + 46.68) / 2
= 47.315
필터링의 결과는 47.315이다.
세 번째 루프
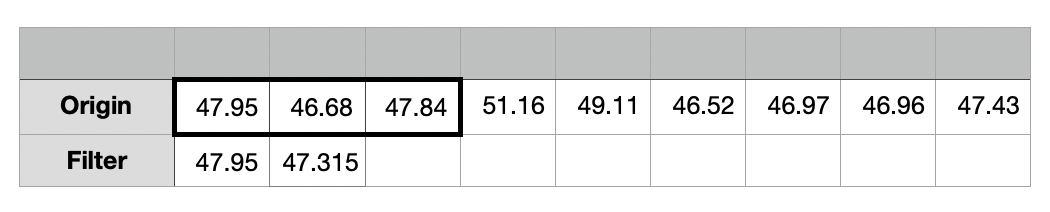

세 번째 루프에서는 버퍼의 크기가 3이고 데이터가 모두 식별되었으므로
= (Origin[0] + Origin[1] + Origin[2]) / (buffer의 요소 개수)
= (47.95 + 46.68 + 47.84) / 3
= 47.49
필터링의 결과는 47.49이다.
네 번째 루프

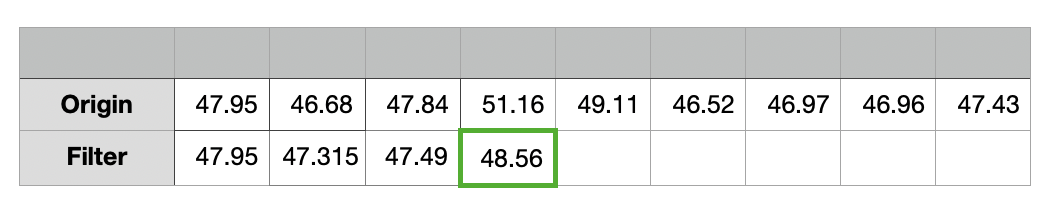
네 번째 루프에서는 버퍼의 크기가 3이고 데이터가 모두 식별되었으며, 버퍼가 한칸씩 시프트되었다.
= (Origin[1] + Origin[2] + Origin[3]) / (buffer의 요소 개수)
= (46.68 + 47.84 + 51.16) / 3
= 48.56
필터링의 결과는 48.56이다.
n번째 루프
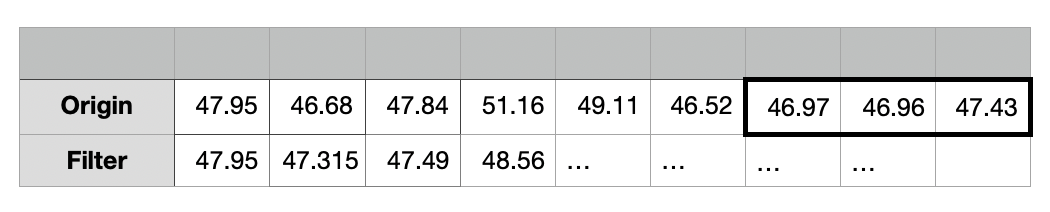
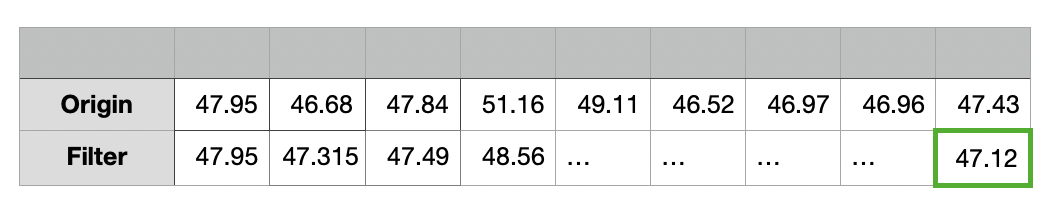
n 번째 루프에서는 버퍼의 크기가 3이고 데이터가 모두 식별되었으며, 버퍼가 n번째 요소까지 시프트되었다.
= (Origin[n - 2] + Origin[n - 1] + Origin[n]) / (buffer의 요소 개수)
= (46.97 + 46.96 + 47.43) / 3
= 47.12
필터링의 결과는 47.12이다.
필터링 결과 비교
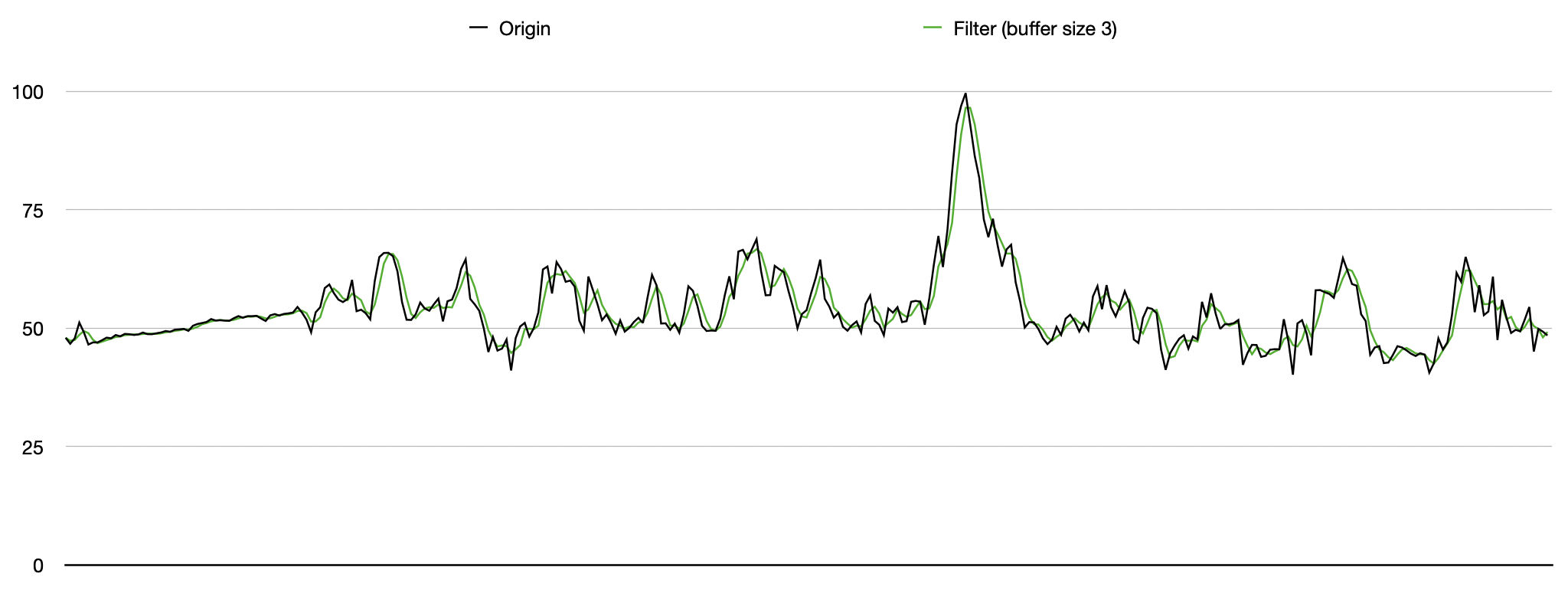
표족하게 튄 원본 데이터에 비해 필터링된 데이터는 변화량이 비교적 완만해진 것을 볼 수 있다.
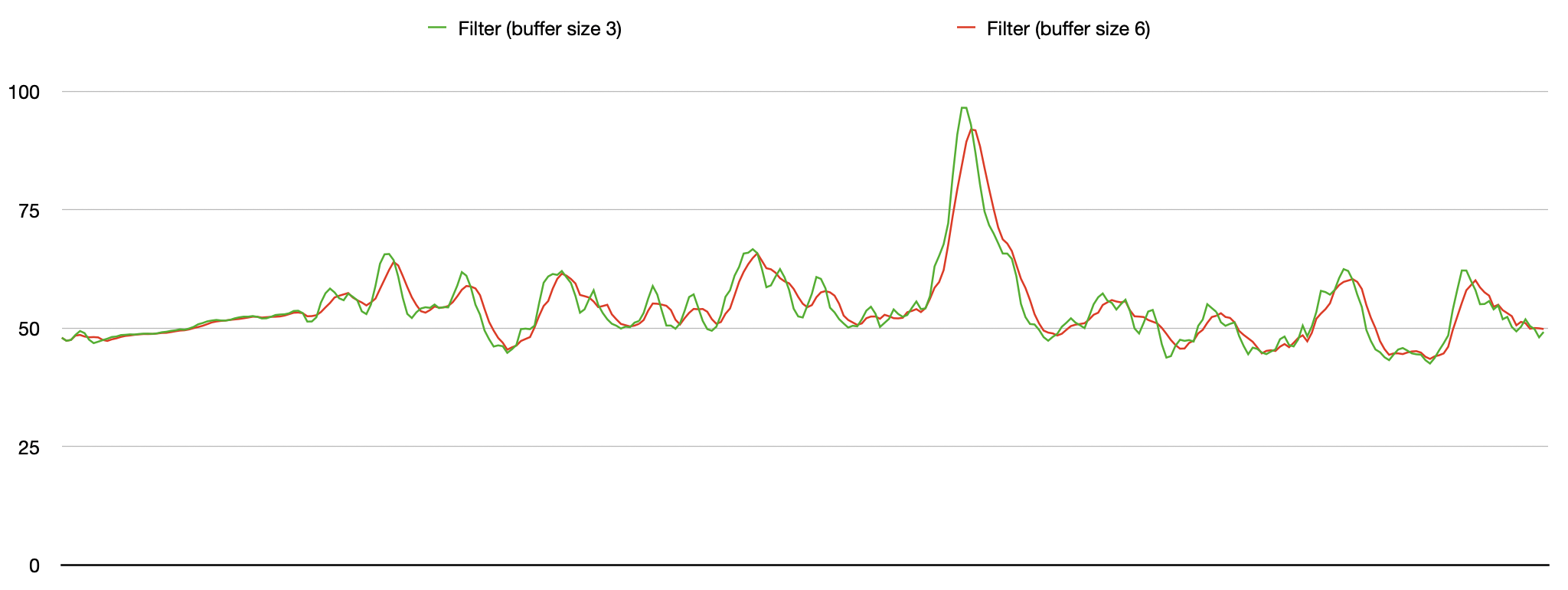
버퍼의 사이즈를 늘려주면 더 완만해진 데이터로 필터링 할 수 있다.
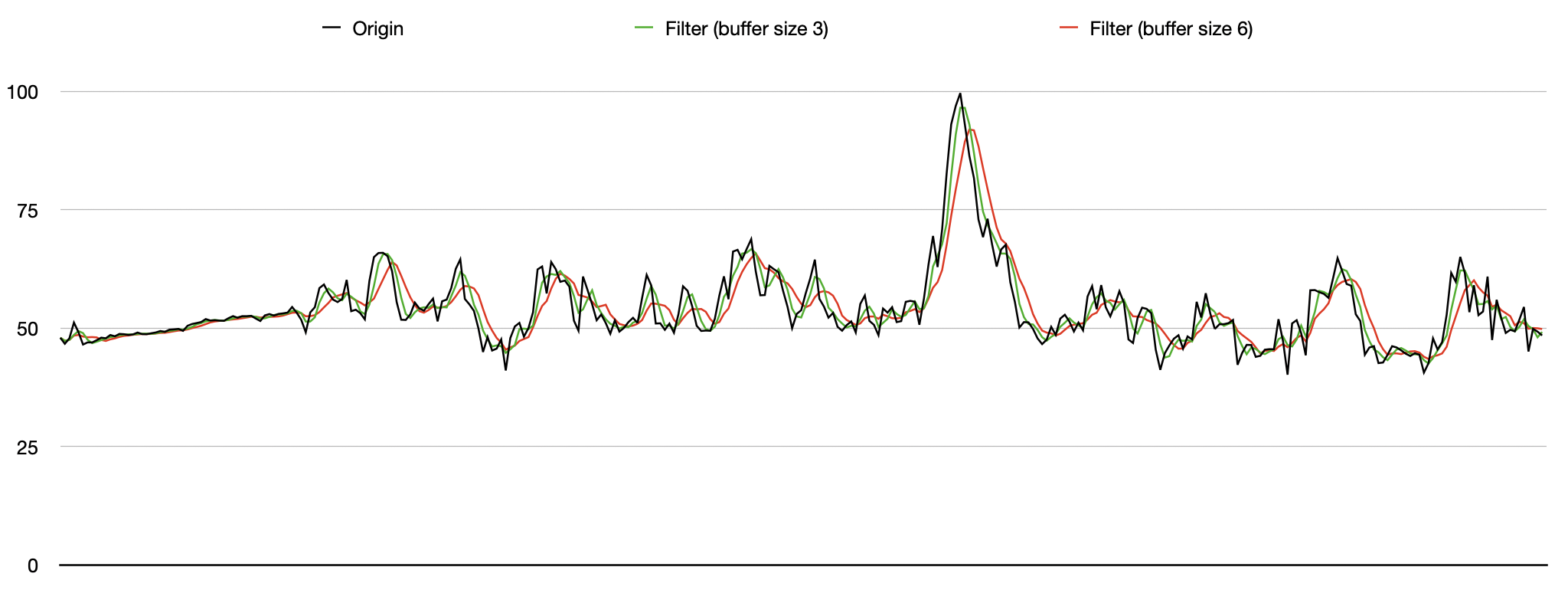
각 필터링 결과를 원본 데이터와 비교해보면 버퍼의 사이즈가 클 수록 노이즈가 많이 제거되었다는 것을 알 수 있다.
그러나 버퍼의 사이즈가 크면 데이터 변동의 반응이 늦어진다. 사진을 보면 버퍼의 사이즈가 클 수록 데이터가 뒤로 밀린 것을 확인할 수 있다.
따라서 스트리밍 데이터처럼 실시간으로 사용되는 데이터에 이동 평균 필터를 적용하려는 경우엔 주의가 필요하다.
소스코드
구현 소스코드는 다음과 같다.
import * as buffer from "buffer";
class MovingAverageFilter {
_size;
_buffer;
/**
* Initialize MAF
*
* @param _size buffer window size
*/
constructor(size) {
if (typeof size !== 'number') {
throw new Error('size must be number.');
}
this._size = size;
this._buffer = [];
}
/**
* Push data to buffer
*
* @param data
*/
push(data) {
if (typeof data !== 'number') {
throw new Error('data must be number.');
}
this._buffer.push(data);
if (this._size < this._buffer.length) {
// remove first element
this._buffer.splice(0, 1);
}
return this.average();
}
/**
* Get average of buffer
*
* @returns {number}
*/
average() {
let count = 0;
let sum = 0;
for (let i = 0; i < this._buffer.length; i++) {
const element = this._buffer[i];
if (Number.isFinite(element) && !Number.isNaN(element)) {
count++;
sum += element;
}
}
return sum / count;
}
}
export default MovingAverageFilter;
push를 할 때마다 버퍼에 담긴 데이터의 평균을 계산하고, 버퍼가 꽉 찼으면 제일 오래된 데이터를 비우고 시프트 후 새 데이터로 채워주는 알고리즘이다.
import MovingAverageFilter from "./moving_average_filter.js";
import * as fs from "fs";
// sample 데이터를 배열 형태로 로딩
const sampleFile = fs.readFileSync('sample.csv', 'utf8');
const sampleDatas = sampleFile.toString().split('\n').map(data => Number(data));
// buffer size가 3인 필터 객체 생성
const movingAverageFilter = new MovingAverageFilter(3);
const results = [];
// 필터링 진행
for (let i = 0; i < sampleDatas.length; i++) {
const origin = sampleDatas[i];
const filtered = movingAverageFilter.push(origin);
results.push(filtered);
}
실사용은 위 코드처럼 필터링하고 싶은 데이터를 순차적으로 집어넣으면 된다. (변수 results)
참고 자료
Moving average - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search type of statistical measure over subsets of a dataset Smoothing of a noisy sine (blue curve) with a moving average (red curve). In statistics, a moving average (rolling average or runn
en.wikipedia.org
'Programming > Algorithm' 카테고리의 다른 글
| [Algorithm] Leaky bucket (처리량 제어기) (0) | 2025.03.11 |
|---|---|
| [Algorithm] 선형 보간법 (Linear interpolation) (0) | 2021.04.22 |
| [Algorithm] 지구에서 두 점 사이의 중간지점 구하기 (1) | 2020.09.15 |
| [Algorithm] 지구에서 두 점 사이의 방위각 구하기 (0) | 2020.09.07 |
| [Alogrithm] 지구에서 두 점 사이의 거리 구하기 (2) | 2020.08.25 |




댓글